Question

mary pitches a ball. the initial height is 4 ft and velocity 55 ft per second. when will the ball hit the ground?

Answer 1

t = 3.5 sec

Explanation:

The equation that represents the position of the ball as a function of time is the following:

`h(t) =P_(o) + V_(o)t+(1)/(2)2at^2`

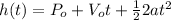
Where:

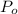`P_(o)` = Initial position of the ball (4 feet tall)

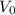`V_(0)` = Initial speed of the ball (55feet / s)

a = acceleration (9.8
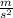`(m)/(s^2)`, or in this case 32.16
`(ft)/(s^2)`)

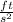t = time in seconds

Then we want to know how long it takes to get to the ground, for this we equal h (t) = 0 and clear t.

So:

`0 = 4 + 55t -16.08t ^ 2`

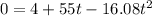
Solving the second degree equation we have:

`(-b+√(b ^ 2-4ac))/(2a) \\ (-b-√(b ^ 2-4ac))/(2a)`

`(-55+√(55^2-4 (-16.08) 4))/(2 (-16.08))= -0.0712\\(-55-√(55^2-4 (-16.08) 4))/(2 (-16.08)) = 3.492`

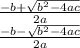
t = -0.071 sec

t = 3.5 sec

We must take the positive solution.

So:

t = 3.5 sec