Answer: The required arc length will be 27.5 units.
Step-by-step explanation: We are given to find the arc length with the following information :
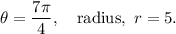
We know that the length of an arc with angle subtended at the center α and radius of the circle r units is given by
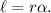
Therefore, the required arc length will be
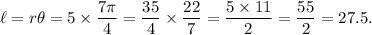
Thus, the required arc length will be 27.5 units.