Question

write the standard form of the equation of the circle with the given characteristics center (4,9) solution point (-8,14)

Answer 1

Answer:
`(\text{x} - 4)^2 + (\text{y}-9)^2 = 169`

============================================================

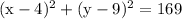
Step-by-step explanation:

Let's find the distance from the center (4,9) to the point on the circle (-8,14)

This distance is the radius of the circle.

`(x_1,y_1) = (4,9) \text{ and } (x_2, y_2) = (-8,14)\\\\d = √((x_1 - x_2)^2 + (y_1 - y_2)^2)\\\\d = √((4-(-8))^2 + (9-14)^2)\\\\d = √((4+8)^2 + (9-14)^2)\\\\d = √((12)^2 + (-5)^2)\\\\d = √(144 + 25)\\\\d = √(169)\\\\d = 13\\\\`

The radius of the circle is r = 13 units.

The center is (h,k) = (4,9)

So,

`(\text{x}-\text{h})^2+(\text{y}-\text{k})^2 = \text{r}^2\\\\(\text{x}-4)^2+(\text{y}-9)^2 = 13^2\\\\(\text{x}-4)^2+(\text{y}-9)^2 = 169\\\\`

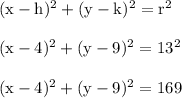
represents the equation of the circle.

You can use graphing tools like Desmos or GeoGebra to confirm. The diagrams of each are shown below as separate images.