Question

Explain how (13 + 10) + 5 is solved differently from 13 + (10 + 5). A) For (13 + 10) + 5, you add 13 + 5 first, then add 10. For 13 + (10 + 5), you add the 10 + 13 first, then add 5. Eliminate B) For (13 + 10) + 5, you add 13 + 10 first, then add 5. For 13 + (10 + 5), you add the 10 + 5 first, then add 13. C) For (13 + 10) + 5, you add 13 - 10 first, then add 5. For 13 + (10 + 5), you add the 10 - 5 first, then add 13. D) For (13 + 10) + 5, you add 13 + 10 first, then subtract 5. For 13 + (10 + 5), you add the 10 + 5 first, then subtract 13.

Answer 1

The answer is B

Explanation:

Simple use P.E.M.D.A.S

Parentheses are always first, you add 13+10 then evaluate everything else.

Have a great day.

Answer 2

B) For (13 + 10) + 5, you add 13 + 10 first, then add 5. For 13 + (10 + 5), you add the 10 + 5 first, then add 13.

Explanation:

Apply the associative property of addition.

Let
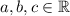`a,b,c\in \mathbb R`, then
`(a+b)+c=a+(b+c)`

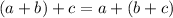
In this case a=13,b=10,c=5.

When we substitute into the above relation, we get:

`(13+10)+5=13+(10+5)`

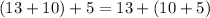
For the LHS, you add 13+5 first, then add 5

For the RHS, you add 10+5 first, then add 13

The correct answer is B