Question

If f(x)=2x+1 and g(x)=x^2-1, find (f/g)(x)

A. x^2 - 7 / 2x + 1
B. 2x + 1 / x^2 - 7
C. 2x + 1 / x^2 - 7, x ≠ ± square root 7
D. x^2 - 7 / 2x + 1, x ≠ - 1/2

Answer 1

Given : f(x)=2x+1 and g(x)=x^2-1.

We need to find (f/g)(x).

Note: In the given options, we have 2x + 1 and x^2 - 7 parts.

So, let us take f(x)=2x+1 and g(x)=x^2-7.

`(f/g)(x) =(f(x))/(g(x))`

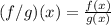
Plugging f and g functions in the formula.

`((f)/(g))(x)=((2x+1))/((x^2-7))`

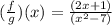
Also, it would be undefined for x = ± square root 7 becaue it would give 0 in the denomiantor.

Therefore, correct option is C. 2x + 1 / x^2 - 7, x ≠ ± square root 7.