Question

Jane bought a car for $30,303. The value of the car depreciated at a constant rate per year. The table below shows the value of the car after the first and second years:

Year 1 2

Value (in dollars) 25,757.55 21,893.92



Which function best represents the value of the car after t years?


f(t) = 25,757.55(0.85)t

f(t) = 30,303(0.85)t

f(t) = 30,303 (0.15)t

f(t) = 25,757.55 (0.15)t

Answer 1

f(t) = 30,303(0.85)^t

Explanation:

The person above is right.

Answer 2

The correct option is 2.

Explanation:

It is given that Jane bought a car for $30,303. The value of the car depreciated at a constant rate per year.

The exponential growth and decay function is defined as

`P=P_0(1+r)^t`

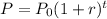
Where, P₀ is initial value and r is growth rate.

The initial value of car is $30,303. Let the rate of depreciation be x%.

`30303-(x)/(100)* 30303=25757.55`

`x=15`

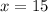
It means rate of depreciation is 15%. Since the value of car decreased by 15% per year, therefore growth rate is -0.15.

`P=30303(1-0.15)^t`

`P=30303(0.85)^t`

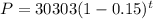
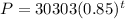
Therefore option 2 is correct.