Answer: The correct option is (C)
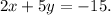
Step-by-step explanation: Given that the equation of the line that passes through (-5, -1) and (10, -7) in point-slope form is given by
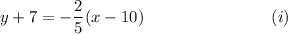
We are to find the standard form of the equation for the above line.
We know that the STANDARD form of the equation of a line is given by
![ax+by=c,~~~~~\textup{[a and b cannot be zero at the same time]}.](https://img.qammunity.org/2019/formulas/mathematics/high-school/t8kj99n6j3z75lqgfrjn6clo58xwigz9tu.png)
From equation (i), we have
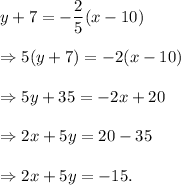
Thus, the required standard form is
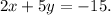
Option (C) is CORRECT.