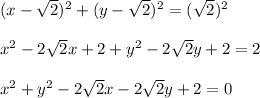Answer:
The equation of
 is:
is:
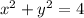
and the equation of
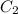 is:
is:
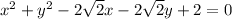
Explanation:
The standard form of circle equation:
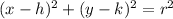 , where
, where
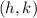 is the center and
is the center and
 is the radius of the circle.
is the radius of the circle.
The center of the circle
 is at origin or at (0, 0) and has radius of 2.
is at origin or at (0, 0) and has radius of 2.
So, the equation of the circle
 will be........
will be........
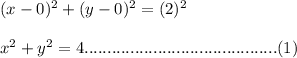
Now, the center of
 is the point in the first quadrant, where the line
is the point in the first quadrant, where the line
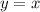 intersects
intersects

Solving the equations
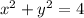 and
and
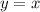 , we will get......
, we will get......
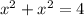 (Substituting
(Substituting
 as
as
 )
)
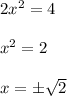
So,
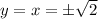
Thus, the center of the circle
 will be at
will be at
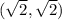 (Negative value is ignored as the point is in first quadrant)
(Negative value is ignored as the point is in first quadrant)
Now, the distance between the center of
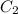 and the x-axis is
and the x-axis is
 and the circle touches the x-axis only at one point.
and the circle touches the x-axis only at one point.
That means, the radius of the circle
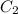 will be also
will be also

So, the equation of the circle
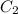 will be......
will be......