a) Let's call x the direction parallel to the river and y the direction perpendicular to the river.
Dave's velocity of 4.0 m/s corresponds to the velocity along y (across the river), while 6.0 m/s corresponds to the velocity of the boat along x. Therefore, the drection of Dave's boat is given by:
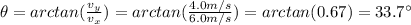
relative to the direction of the river.
b) The distance Dave has to travel it S=360 m, along the y direction. Since the velocity along y is constant (4.0 m/s), this is a uniform motion, so the time taken to cross the river is given by
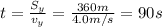
c) The boat takes 90 s in total to cross the river. The displacement along the y-direction, during this time, is 360 m. The displacement along the x-direction is
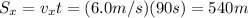
so, Dave's landing point is 540 m downstream.
d) If there were no current, Dave would still take 90 seconds to cross the river, because its velocity on the y-axis (4.0 m/s) does not change, so the problem would be solved exactly as done at point b).