Question

a rectangular rug has a perimeter of 470 yards. the width of the rug is 5 yards more than four times the length. find the length and the width

Answer 1

Width= W, Length = L
perimeter = 2L+2W
470= 2L+2W

W= 4L+5
Substitute this into the perimeter equation
470=2L+2(4L+5)
470=2L+8L+10
470=10L+10
460=10L
Length = 46 yards
Width= (46x4)+5
Width=189 yards

Answer 2

Answer: The required length and breadth of the rug are 46 yards and 189 yards respectively.

Step-by-step explanation: Given that a rectangular rug has a perimeter of 470 yards. The width of the rug is 5 yards more than four times the length.

We are to find the length and width of the rug.

Let l represents the length of the rug. Then, the width of the rug will be

`w=4l+5.`

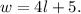
According to the given information, we have

`470=2l+2w\\\\\Rightarrow 470=2l+2(4l+5)\\\\\Rightarrow 470=2l+8l+10\\\\\Rightarrow 10l=460\\\\\Rightarrow l=(460)/(10)\\\\\Rightarrow l=46.`

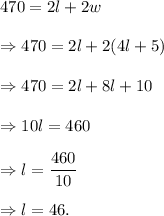
So, the width is given by

`w=4*46+5=184+5=189.`

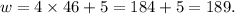
Thus, the required length and breadth of the rug are 46 yards and 189 yards respectively.