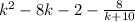So for this, we will be using synthetic division. To set it up, have the equation so that the divisor is -10 (since that is the solution of k + 10 = 0) and the dividend are the coefficients. Our equation will look as such:
(Note that synthetic division can only be used when the divisor is a 1st degree binomial)
- -10 | 1 + 2 - 82 - 28
- ---------------------------
Now firstly, drop the 1:
- -10 | 1 + 2 - 82 - 28
- ↓
- -------------------------
- 1
Next, you are going to multiply -10 and 1, and then combine the product with 2.
- -10 | 1 + 2 - 82 - 28
- ↓ - 10
- -------------------------
- 1 - 8
Next, multiply -10 and -8, then combine the product with -82:
- -10 | 1 + 2 - 82 - 28
- ↓ -10 + 80
- -------------------------
- 1 - 8 - 2
Next, multiply -10 and -2, then combine the product with -28:
- -10 | 1 + 2 - 82 - 28
- ↓ -10 + 80 + 20
- -------------------------
- 1 - 8 - 2 - 8
Now, since we know that the degree of the dividend is 3, this means that the degree of the quotient is 2. Using this, the first 3 terms are k^2, k, and the constant, or in this case k² - 8k - 2. Now what about the last coefficient -8? Well this is our remainder, and will be written as -8/(k + 10).
Putting it together, the quotient is