answer : 15
x varies inversely as y and directly as t
We use formula
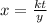
x varies inversely as y so we divide by y
x varies directly as t so we multiply x
k is the constant of proportionality
Lets find out k using the given values
x = 12 when t = 10 and y = 25
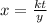
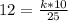
Multiply by 25 on both sides
300 = 10k (divide by 10)
So k = 30
Lets find y when x is 6 and t = 3. we got k = 30
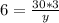 (cross multiply)
(cross multiply)
6y = 90 (divide by 6 )
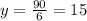
The value of y = 15