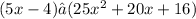Answer:
Explanation:
Factor 125
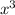 -64
-64
STEP 1: Equation at the end of step 1
5³ₓ³ - 64
STEP 2:
Trying to factor as a Difference of Cubes:
2.1 Factoring: 125
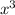 -64
-64
Theory : A difference of two perfect cubes
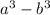 ,can be factored into
,can be factored into
(a-b) • (a² +ab +b²)
Proof : (a-b)•(a²+ab+b²) =
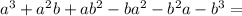
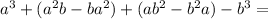
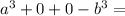
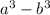
Check : 125 is the cube of 5
Check : 64 is the cube of 4
Check : x³ is the cube of x¹
Factorization is :
(5
 - 4) • (25
- 4) • (25
 + 20
+ 20
 + 16)
+ 16)
Trying to factor by splitting the middle term
2.2 Factoring 25
 + 20
+ 20
 + 16
+ 16
The first term is, 25
 its coefficient is 25 .
its coefficient is 25 .
The middle term is, +20
 its coefficient is 20 .
its coefficient is 20 .
The last term, "the constant", is +16
Step-1 :
Multiply the coefficient of the first term by the constant 25 • 16 = 400
Step-2 :
Find two factors of 400 whose sum equals the coefficient of the middle term, which is 20 .
-400 + -1 = -401
-200 + -2 = -202
-100 + -4 = -104
-80 + -5 = -85
-50 + -8 = -58
-40 + -10 = -50
For tidiness, printing of 24 lines which failed to find two such factors, was suppressed
Observation : No two such factors can be found !!
Conclusion : Trinomial can not be factored
Final result :