Question

#34. Find the value of x for the rectangle.

(How did u do it/what did u do)

Answer 1

Hey, CadenClough! For this, it's best to use algebra. We know that rectangles have two of each measure: two lengths and two widths. This means the formula to find the complete perimeter of the rectangle is 2l + 2w = p.

Now let's look at the problem. For length, we have x + 3 and for width we have 2x - 6. First off, fill in the values for length and width in the perimeter equation like this:

`2(x + 3) + 2(2x - 6) = 26`

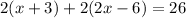
Now distribute the 2:

`--> 2x + 6 + 4x - 12 = 26`

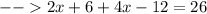
Combine like terms:

`2x + 4x + 6 - 12 = 26`

Simplify:

`6x - 6 = 26`

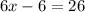
Isolate x:

`6x = 26 + 6`

-->
`x = (32)/(6)`

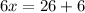
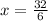
Now plug in the value of x:

`2((32)/(6) + 3) + 2(2 * (32)/(6) - 6)`

= 64/3 - 12 + 32/3 + 6

= 26

So x =
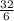`(32)/(6)` or 16/3.