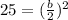Question

James is solving the equation x^2+10x=50 by completing the square. What number must be added to both sides of the equation to complete the square?

Answer 1

Let f (x) be a quadratic equation of the form:

`x^2+bx+c\\`

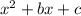
Where b and c are real numbers.

So a generic procedure for completing squares is:

1) identify b

In this case b = 10

2) divide b between 2 and then square it

`((b)/(2))^ 2\\`

`((10)/(2))^ 2=25\\`

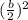
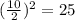
3) Add and subtract
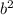`b ^ 2` in the equation

`x ^2+10x + 25 - 25 = 50\\`

`x ^ 2 + 10x +25 = 75\\`

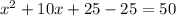
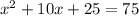
4) Rewrite the equation as follows

`(x+(b)/(2))^2=c\\`

`(x + 5) ^ 2 = 75\\`

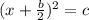
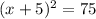
The number that you must add to both sides of the equation is number
`25 = ((b)/(2))^2`