Answer:
Sami should invest in 1st case, to get the maximum money.
Explanation:
Sami has $500 to invest.
We will use the compound interest formula :

Case 1:
p = 500
r = 3% or 0.03
t = 4
n = 1
Putting the values in formula we get,
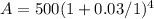
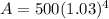
A = $562.75
Case 2:
p = 500
r = 4% or 0.04
n = 1
t = 3
Putting the values in formula we get,


A = $562.43
Case 3:
p = 500
r = 2.5% or 0.025
n = 3
t = 6
Putting the values in formula we get,
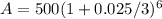
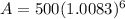
A = $525.42
Case 4:
p = 500
r = 5% or 0.05
n = 1
t = 2
Putting the values in formula we get,
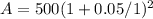
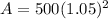
A = $551.25
Comparing all values we can see that case 1 has the highest amount.
Hence, Sami should invest in 1st case, to get the maximum money.