Question

Find the minimum value of C=-2x+y subject to the following constraints x≥-5 x≤4 y≥-1 x≤3

Answer 1

The minimum value of C is -9

Explanation:

we have

`C=-2x+y`

`x\geq -5`

`x\leq 4`

`y\geq -1`

`y\leq 3`

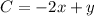
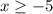
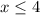
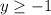
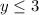
using a graphing tool

The solution is the shaded rectangle

see the attached figure

The vertices of the rectangle are the points

`(-5,3),(4,3),(4,-1),(-5,-1)`

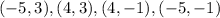
To find the the minimum value of C, substitute the value of x and the value of y of each vertex and calculate the value of C, then compare the results

For
`(-5,3)`

`C=-2(-5)+3=13`

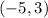
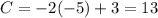
For
`(4,3)`

`C=-2(4)+3=-5`

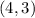
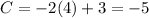
For
`(4,-1)`

`C=-2(4)-1=-9`

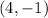
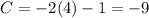
For
`(-5,-1)`

`C=-2(-5)-1=9`

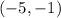
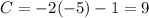
therefore

The minimum value of C is -9