Question

In how many ways can the 19 members of a chess club fill the offices of​ King, Knight,​ Bishop, and​ Rook?

Answer 1

This problem is a permutation because the order matters here. This means that choosing A as King, B as Knight, C as Bishop and D as Rook results in a different arrangement from B as King, A as Knight, D as Bishop and C as Rook. We would count them both because in the first case A is King, but in the second case A is Knight.

Therefore, the possible number of ways are given below:

`19P4=(19!)/((19-4)!) =(19 * 18 * 17 * 16 * 15!)/(15!) =19 * 18 * 17 * 16 =93024`

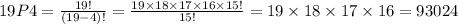
Hence there will be 93024 ways 19 members of a chess club fill the offices of King, Knight, Bishop, and Rook.