Answer:
Option B: 25 inches, 60 inches and 65 inches is the correct answer.
Explanation:
We will use Pythagorean theorem to find out the dimensions that Adam should use.
A. 50 in, 110 in and 130 in
Using Pythagorean theorem;
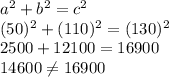
These dimensions will not form a right triangle.
B. 25 in, 60 in, and 65 in
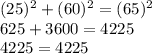
These dimensions of the frame will form a right triangle.
C. 40 in., 44 in., 58 in.
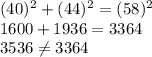
These dimensions will not form a right angled triangle.
D. 130 in., 50 in, 60 in
The larger dimension represents the hypotenuse in right angled triangle.
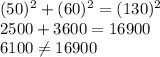
These dimensions will not form a right angled triangle.
Hence,
Option B: 25 inches, 60 inches and 65 inches is the correct answer.