Question

What are the x- and y-intercepts of the graph of y = x2 + 3x − 10? x-intercepts: (−2, 0) and (5, 0) y-intercept: (0, 10) x-intercepts: (−2, 0) and (−5, 0) y-intercept: (0, 10) x-intercepts: (−2, 0) and (5, 0) y-intercept: (0, −10) x-intercepts: (2, 0) and (−5, 0) y-intercept: (0, −10)

Answer 1

2, 0) and (−5, 0)

Explanation:

Answer 2

We have the following function:

`f(x)=x^2+3x-10`

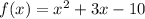
So, we need to find the x- and y-intercepts of the graph of that function, therefore:

1. x-intercepts

x-intercepts can be found when
`y=0`, so:

`0=x^2+3x-10 \\ \\ Using \ Quadratic \ Formula \\ \\ x=(-b \pm √(b^2-4ac))/(2a) \\ \\ Where: \\ \\ a=1, b=3, c=-10 \\ \\ x=(-3 \pm √(3^2-4(1)(-10)))/(2(1)) \\ \\ Two \ values: \\ \\ x=2 \ and \ x=-5`

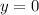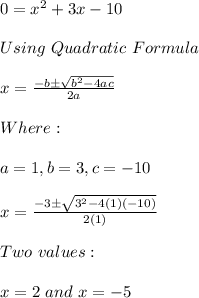
So, the x-intercepts are:

`\boxed{(2,0) \ and \ (-5, 0)}`

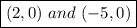
2. y-intercepts

x-intercepts can be found when
`x=0`, so:

`y=(0)^2+3(0)-10 \\ \\ \therefore y=-10`

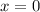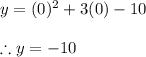
So, the y-intercept is:

`\boxed{(0,-10)}`

_______________________________________

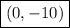
Therefore the right answer is:

x-intercepts: (2, 0) and (−5, 0) y-intercept: (0, −10)

This is indicated in the Figure bellow.