Question

I need help with this ​

Answer 1

Here is the summary of true statements:

A) The statement of the function modeled is (0, 3) is TRUE.

D) the equation for the line function is y = 2x+3 is TRUE.

E) the given table represents the linear function is TRUE

Explanation:

Given the table

x 1 3 5 7

y 5 9 13 17

E)

It is clear that there is a CONSTANT CHANGE in the x and y values of the graph.

THE CONSTANT CHANGE IN X VALUES

i.e. 3-1=2, 5-3=2, 7-5=2

THE CONSTANT CHANGE IN Y VALUES

i.e. 9-5 = 4, 13 - 9 = 4, 17 - 13 = 4

Thus, the given table represents the linear function is TRUE

B)

It is clear that the value of y increase as the value of x increases.

Thus, the statement ''the value of y decreases as the value of x increases'' is FALSE!

D)

We know that the slop-intercept form of the line equation is

`y = mx+b`

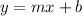
where m is the slope and b is the y-intercept.

Determining the equation

Taking two points

(1, 5)

(3, 9)

Finding the slope between (1, 5) and (3, 9)

Using the formula

Slope = m = [y₂ - y₁] / [x₂ - x₁]

= [9 - 5] / [3 - 1]

= 4 / 2

= 2

Thus, the slope of the line = m = 2

now substituting m = 2 and the point (1, 5) to determine the y-intercept

y = mx+b

5 = 2(1) + b

b = 5-2

b = 3

Thus, the value of y-intercept b = 3

substituting b = 3 and m = 2 in the slope-intercept form

y = mx+b

y = 2x+3

Therefore, the equation for the line function is y = 2x+3 is TRUE

A)

We know that the value of the y-intercept can be determined by setting x = 0, and determining the corresponding value of y.

We already know that the y-intercept b = 3

It means the y-intercept modeled is (0, 3)

Therefore, the statement of the function modeled is (0, 3) is TRUE.

C)

We have already got the equation

y = 2x+3

substituting x = 8

y = 2(8)+3

y = 10+3

y = 13

so at x = 8, the value of y = 13

Therefore, the statement that the ''On a graph of the function when x = 8, the value of y will be 2'' is FALSE!

Conclusion:

Here is the summary of true statements:

A) The statement of the function modeled is (0, 3) is TRUE.

D) the equation for the line function is y = 2x+3 is TRUE.

E) the given table represents the linear function is TRUE