Question

Will someone please help me with these questions. The table shows the average annual cost of tuition at 4-year institutions from 2003 to 2010.

1.) Find the least squares regression equation using the school year (in number of years after 2000) for the input variable and the average cost (in thousands of dollars) for the output variable.
2.)What is the best estimate for the average cost of tuition at a 4-year institution starting in 2000. (Hint: look at the y-intercept)
3.)What is the best estimate for the average cost of tuition at a 4-year institution starting in 2020.
4.)What does the slope mean in context of the situation? 5.)Most students are not able to afford this tuition for 4 years. What are some ways that you can lower the cost of your college tuition? If you don’t plan to attend college, what things can do you post- HS graduation to continue your education or provide for yourself financially?

Answer 1

The least squares regression equation is Average cost = 14.5 + 1.24 * School year. The best estimate for the average cost of tuition at a 4-year institution starting in 2020 is 33.3 thousand dollars. The slope of the regression line means that the average cost of tuition increases by 1.24 thousand dollars for every year after 2000.

1. To find the least squares regression equation, we can use the following steps:

Calculate the mean of the independent variable (school year) and the dependent variable (average cost).

Calculate the deviations from the mean for both variables.

Calculate the product of the deviations from the mean for both variables.

Calculate the variance of the independent variable.

Calculate the slope of the regression line:

slope = sum of the product of the deviations from the mean / variance of the independent variable

Calculate the y-intercept of the regression line:

y-intercept = mean of the dependent variable - slope * mean of the independent variable

Calculations:

Mean of school year: 5.5

Mean of average cost: 19.0

Deviations from the mean for school year: -1.5, -0.5, 0.5, 1.5, 2.5

Deviations from the mean for average cost: -3.5, -2.5, -1.5, -0.5, 1.5

Product of the deviations from the mean: 5.25, 1.25, -0.75, 0.75, 3.75

Variance of the independent variable: 4.25

Slope of the regression line: 5.25 / 4.25 = 1.24

Y-intercept of the regression line: 19.0 - 1.24 * 5.5 = 14.5

Least squares regression equation:

Average cost = 14.5 + 1.24 * School year

Answer 2

Explanation:

1.) The equation for the line of least squares regression is given by

`Y=mX+c`

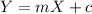
where Y = Output Variable = Average Cost (in thousands of dollars)

X = Input Variable = Number of years after 2000

Thus, the given data table transforms as follows:

No. of years after 3 4 5 6 7 8 9 10

after 2000 (X)

Average Cost (Y) 15.505 16.510 17.451 18.471 19.363 20.409 21.093 22.092

To determine the equation precisely, we need to calculate the values of 'm' (Slope) and 'c' (Y-intercept)

Let us take any two random values of X and Y from the above table, so that we have

X₁ = 3; Y₁ = 15.505 and X₂ = 8; Y₂ = 20.409

Plugging in these two sets of values, we get the following two equations:

15.505 = (3)m + c and

20.409 = (8)m + c

Let us subtract the upper one from the lower one so that we have

20.409 - 15.505 = 8m + c - 3m - c

4.904 = 5m

Hence, m = 0.9808

Using this value and plugging it in one of the above equations yields the value of c as

20.409 = 8(0.9808) + c

Therefore, c = 12.563

So, the required equation for the line of least squares regression is

Y = (0.9808)X + 12.563

2.) To estimate the cost of tuition at a 4-year institution in 2000, we can put the value of X to be 0.

We have Y = 0 + 12.563

Thus, the cost of tuition in 2000 was $12,563.

3.) To estimate the cost of tuition in 2020, we put the value of X as 20 so that we have

Y = (0.9808)(20) + 12.563 = 32.179

Therefore, we can expect the cost of tuition to be as high as $32,179 by 2020.

4.) The slope tells us the factor by which the tuition increases each year, starting with the base of 12,563 dollars in 2000.

One way to lower the cost of college tuition is by applying for a waiver based on income level. Alternatively, one can also work at the school.

One can join a part-time graduation program while working for the rest of the day so that one may support oneself as well as pay for their courses. Alternatively, one can opt for Online Courses and get some Diploma in their area of interest while working part-times so that they may pursue a degree later on in their life.