Answer:
z-score will be: 7.741.... and it will be unusual.
Explanation:
Human body temperatures have a mean of 98.20 degrees Fahrenheit and a standard deviation of 0.62 degrees Fahrenheit.
So here,
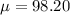 and
and
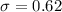
Formula for z-score is:
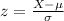
Thus, the z-score for 103.00 degrees Fahrenheit will be.......
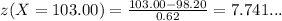
As, here the z-score is more than 2 standard deviations above the mean, so 103.00 degrees Fahrenheit is unusual for human body temperature.