Question

In △ABC the angle bisectors drawn from vertices A and B intersect at point D. Find ∠ADB if: c ∠C=130°

Answer 1

Answer = 155 degrees

Answer 2

In Δ ABC, let A = x°

By Angle-sum property,

A + B + C = 180°

But, it is given that C = 130°

So, x + B + 130 = 180

B = 180 - 130 - x

B = 50 - x

Since AD and BD are internal bisectors of A and B,

∠ DAB = x/2 and

∠ DBA =
`(50-x)/(2)`

`=25-(x)/(2)`

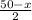
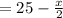
In Δ ADB, by angle-sum property,

∠ DBA + ∠ DAB +∠ ADB = 180°

`=(25-(x)/(2) )+(x)/(2) +` + ∠ ADB = 180°

25 + ∠ ADB = 180°

∠ ADB = 180 - 25 = 155°

Hence, ∠ ADB = 155°.