Question

Alma invests $300 in an account that compounds interest annually. After 2 years, the balance of the account is $329.49. To the nearest tenth of a percent, what is the rate of interest on the account?

Answer 1

Invested amount (P) = $300.

Time in years (t) = 2 years.

Balance after 2 years (A) = $329.49.

Let us assume rate of interest = r % compounds annually.

We know, formula for compound interest

`A=P(1+r)^t`

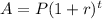
Plugging values in formula, we get

`329.49=300(1+r)^2`

`\mathrm{Divide\:both\:sides\:by\:}300`

`(300\left(1+r\right)^2)/(300)=(329.49)/(300)`

`\left(1+r\right)^2=1.0983`

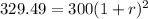
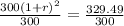
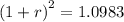
Taking square root on both sides, we get

`1+r=√(1.0983)`

`\mathrm{Subtract\:}1\mathrm{\:from\:both\:sides}`

`1+r-1=√(1.0983)-1`

`r=√(1.0983)-1`

`r=1.048-1`

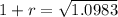
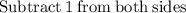
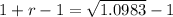
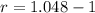
r=0.048.

Converting it into percentage by multiplying by 100.

r=0.048 × 100

r = 4.8 %

Therefore, the rate of interest on the account is 4.8% compounds annually.