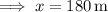Question

michael kicks a ball at an angle if 36* horizontal. its initial velocity is 46 m/s. Find the maximum height it can reach, total time, and horizontal displacement for this motion

Answer 1

(a) At its maximum height, the ball's vertical velocity is 0. Recall that

`{v_y}^2-{v_(0y)}^2=2a_y\Delta y`

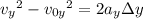
Then at the maximum height
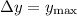`\Delta y=y_{\mathrm{max}}`, we have

`-\left(\left(46\,(\mathrm m)/(\mathrm s)\right)\sin36^\circ\right)^2=2\left(-9.8\,(\mathrm m)/(\mathrm s^2)\right)y_{\mathrm{max}}`

`\implies y_{\mathrm{max}}=37\,\mathrm m`

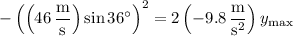
(b) The time the ball spends in the air is twice the time it takes for the ball to reach its maximum height. The ball's vertical velocity is

`v_y=v_(0y)+a_yt`

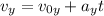
and at its maximum height,
`v_y=0` so that

`0=\left(46\,(\mathrm m)/(\mathrm s)\right)\sin36^\circ+\left(-9.8\,(\mathrm m)/(\mathrm s)\right)t`

`\implies t=2.8\,\mathrm s`

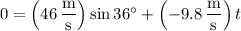
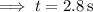
which would mean the ball spends a total of about 5.6 seconds in the air.

(c) The ball's horizontal position in the air is given by

`x=v_(0x)t`

so that after 5.6 seconds, it will have traversed a displacement of

`x=\left(46\,(\mathrm m)/(\mathrm s)\right)\cos36^\circ(5.6\,\mathrm s)`

`\implies x=180\,\mathrm m`