Question

A chemist is studying the properties of a gas under various conditions. He observes that when the gas is at room temperature and low pressure, it behaves as an ideal gas. When the gas is cooled to 10 kelvin and is placed under high pressure, however, it deviates significantly from an ideal gas. Explain these observations

Answer 1

Answer: A, B, & C

Step-by-step explanation:

A. The ideal gas model assumes that gas particles experience no intermolecular attractions and these forces cause the gas to deviate from ideal behavior.

B. At very low temperatures, gas particles move slowly.

C. At very high pressures, gas particles are very close together.

Got it right on edge :)

Answer 2

An ideal gas is a theoretical concept and a real gas behaves in an ideal manner under conditions which includes a high temperature and a low pressure such that the gas has high kinetic energy, and the intermolecular forces between the molecules are weak

The Ideal Gas Law is P·V = n·R·T

Where;

P = The pressure of the gas

V = The volume of the gas

n = The number of moles of the gas

R = The Universal Gas Constant

T = The temperature of the gas

For a gas cooled to 10 Kelvin and placed under high pressure, the interaction between individual gas molecules increases, and the kinetic energy of the gases is much lower and more comparable to the inter molecular forces between the gas molecules, which in turn produces observable changes from the initial ideal behavior of the gas such that the gas behavior deviates from the Ideal Gas Laws appreciably and are better modelled by the Van der Waals Equations which takes into account, the volume the gas particles occupy and the intermolecular forces between the molecules

The Van der Waals equation is presented as follows;

`P = (R \cdot T)/(V - b) - (a)/(V^2)`

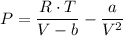
Where;

V = The molar volume

a = The gas constant a represents the attractive forces between the gas particles

b = Represent the volume occupied by the particles of the gas

Step-by-step explanation: