Question

The straight line joining the points A(3,-5) and B(6,k) has a gradient of 4. Work out the value of k.

Answer 1

The straight line joining the points A(3,-5) and B(6,k) has a gradient of 4.

Gradient is the slope

So the slope of the line joining the points A(3,-5) and B(6,k) is 4

Slope of line joining two points =
`(y_2-y_1)/(x_2-x_1)`

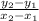
A(3,-5) and B(6,k) are (x1,y1) and (x2,y2)

slope =
`(y_2-y_1)/(x_2-x_1)`

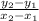
slope =
`(k-(-5))/(6-3)=(k+5))/(3)`

We know slope =4

`(k+5))/(3)=4`

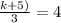
Cross multiply and solve for k

k + 5 = 12

k = 7

The value of k = 7