Question

Write An equation in slope intercept form for the line passing through each pair of points (-1,3) and (2,-5)

Answer 1

Slope intercept form of a line is y = mx + b, where m is the slope and b is the y coordinate of the y intercept.

The easiest way to solve this problem is by using another equation for a line, also known as point slope form. This equation is best to use for a line if you have a point and slope of the line, but do not have the y-intercept.

We need to find the slope of this line passing through the pair of points (-1, 3) and (2, -5). We can do this by using the slope formula:
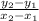`(y_2-y_1)/(x_2-x_1)`. Substitute in the appropriate coordinates.

`(-5-3)/(2-(-1))` =
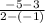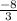`(-8)/(3)`, so the slope of the line is -8/3.

Point slope form of a line is
`y-y_1=m(x-x_1)`. Substitute -8/3 for m, and use the point coordinate (-1, 3) for y1 and x1. You could use either point coordinate but I chose to use this one.

`y-3= -8/3[x-(-1)]`

Distribute -8/3 inside the parentheses.

`y-3= -8/3x - 8/3`

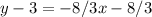
Add 3 to both sides.

y = -8/3x + 1/3 is your answer (slope intercept form).

Answer 2

Slope m = y2-y1/x2-x1

Points (-1,3) and (2,-5)

M= -5-3/2-(-1)

M= -8/3

M= -8/3

Slope is -8/3

Now fill in the formula equation of a line using one if the points and slope to find b .

(2,-5) and slope -8/3

Y=mx+b

-5=-8/3(2)+b

-5=-16/3+b

-5+16/3=b

1/3=b

Now put all together

Y= -8/3x+1/3