Question

Airbags are manufactured by Aces (A), Best (B), and Cool (C) at rates of 57%, 26% and 17%, respectively. Airbags occasionally kill (K) passengers when they deploy in accidents. Airbags made by Aces, Best, and Cool do not kill people at rates of 99%, 96%, and 87%, respectively. One airbag is randomly selected for testing.

If an airbag kills a passenger, calculate the probability that the airbag was manufactured by Cool. (Round to the nearest ten-thousandth.)

Answer 1

Air bag manufactured by Aces(A)=57%

So, Probability
`P(A)=(57)/(100)`

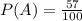
Air bag manufactured by Best (B) =26%

So, Probability
`P(B)=(26)/(100)`

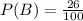
Airbag manufactured by Cool(C)=17%

So, Probability
`P(C)=(17)/(100)`

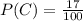
Airbags made by Aces, Best, and Cool do not kill people at rates of 99%, 96%, and 87%, respectively.

Let K be the event which kill people.

Probability of Air bag made by A which kill people
`P(K/A)=(1)/(100)`

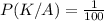
Probability of Air bag made by B which kill people
`P(K/B)=(4)/(100)`

Probability of Air bag made by C which kill people
`P(K/A)=(13)/(100)`

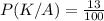
If an airbag kills a passenger, calculate the probability that the airbag was manufactured by Cool

Using Baye's theorem:

`P(C/K)=(P(K/C)P(C))/(P(K/A)P(A)+P(K/B)P(B)+P(K/C)P(C))`

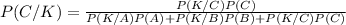
Substitute the values of probabilities into formula

We get,

`P(C/K)=(0.17* 0.13)/(0.57* 0.01+0.26* 0.04+0.17* 0.13)`

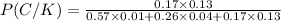
Now we calculate it and get probability

So,
`P(C/K)=0.5785`

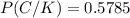
So, 57.85% of passenger kills if the airbag was manufactured by Cool.