Question

The table shows the average annual cost of tuition at 4-year institutions from 2003 to 2010.

What is the best estimate for the average cost of tuition at a 4-year institution starting in 2020. (Hint: Use the graph from desmos, or your equation from part A).

What does the slope mean in context of the situation?

Answer 1

Answer: 1) The best estimate for the average cost of tuition at a 4-year institution starting in 2020 =$ 31524.31

2) The slope of regression line b=937.97 represents the rate of change of average annual cost of tuition at 4-year institutions (y) from 2003 to 2010(x). Here,average annual cost of tuition at 4-year institutions is dependent on school years .

Explanation:

1) For the given situation we need to find linear regression equation Y=a+bX for the given situation.

Let x be the number of years starting with 2003 to 2010.

i.e. n=8

and y be the average annual cost of tuition at 4-year institutions from 2003 to 2010.

With reference to table we get

`\sum x=36\\\sum y=150894\\\sum x^2=204\\\sum xy=718418`

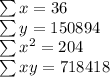
By using above values find a and b for Y=a+bX, where b is the slope of regression line.

`a=((\sum y)(\sum x^2)-(\sum x)(\sum xy))/(n(\sum x^2)-(\sum x)^2)=(150894(204)-(36)718418)/(8(204)-(36)^2)=(30782376-25863048)/(1632-1296)=(4919328)/(336)\\\\=14640.85`

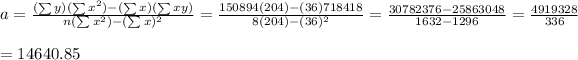
and

`b=(n(\sum xy)-(\sum x)(\sum y))/(n(\sum x^2)-(\sum x)^2)=(8(718418)-(36)150894)/(8(204)-(36)^2)=(5747344-5432184)/(1632-1296)=(315160)/(336)\\\\=937.97`

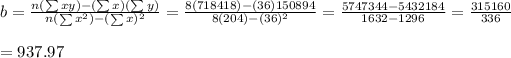
∴ To find average cost of tuition at a 4-year institution starting in 2020.(as n becomes 18 for year 2020 if starts from 2003 ⇒X=18)

So, Y= 14640.85 + 937.97×18 = 31524.31

∴The best estimate for the average cost of tuition at a 4-year institution starting in 2020 = $31524.31