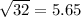Answer:
b = 5.65
Explanation:
Since it's a right triangle, we can apply the Pythagorean theorem.
We know that the hypotenuse is 9, and one leg is 7. We are missing the other leg which is called b.
The Pythagorean theorem tells us that if the hypotenuse is c and the legs of the right triangle are a and b, then we have
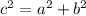
So we're going to solve this formula for the values given c= 9 and a = 7
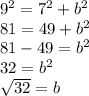
Thus, b =