You can use simultaneous linear equations in two variables to solve this word problem.
Let Juwan's age be
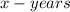
and Christy's age be
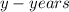
Let us sum their ages and equate it to 92
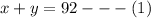
Ten years ago, Juwan's age was
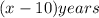
and Christy's age was
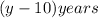
By then Juwan's age was 3 times Christy's age
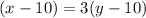
Expand and simplify,
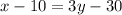

Put equation (2) in equation (1)
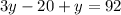
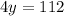

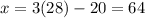
Juwan is 64 now