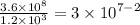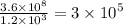Question

What is the value of the expression All of 3.6 multiplied by 10 to the power 8 over all of 1.2 multiplied by 10 to the power 3? 2.4 × 105 3.0 × 1011 3.0 × 105 2.4 × 1011

Answer 1

You have to use the laws of exponents and your knowledge of multiplication by 10.

So we have

`\frac{3.6 * {10}^(8) }{1.2 * {10}^(3) }`
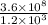
We can rewrite like this



`\frac{3.6 * {10}^(8) }{1.2 * {10}^(3) } = \frac{3.6 * 10 * {10}^(7) }{1.2 * 10 * {10}^(2) }`

So multiplying by the 10 will get read of the decimal


`\frac{3.6 * {10}^(8) }{1.2 * {10}^(3) } = \frac{36 * {10}^(7) }{12 * {10}^(2) }`

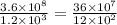
Now divide the 36 by 12 , write one base of 10 subtract and the exponent of 2 from 7


`\frac{3.6 * {10}^(8) }{1.2 * {10}^(3) } = 3 * {10}^(7 - 2)`


`\frac{3.6 * {10}^(8) }{1.2 * {10}^(3) } = 3 * {10}^(5)`

Answer 2

Option C is the correct answer.

Explanation:

We have to find the value of
`(3.6* 10^8)/(1.2* 10^3)`

Determining

`(3.6* 10^8)/(1.2* 10^3)=(3.6)/(1.2)* (10^8)/(10^3)=3* 10^(8-3)\\\\(3.6* 10^8)/(1.2* 10^3)=3* 10^5`

Option C is the correct answer.