Question

I can't seem to solve this :

log(x-3)·log(x)
---------------------- ≤ 0
log(x-4)


I would love a good explanation of the resolution process

Answer 1

`D:x-3>0 \wedge x>0 \wedge x-4>0 \wedge \log(x-4)\\ot=0\\D:x>3 \wedge x>0 \wedge x>4 \wedge x-4 \\ot=1\\D:x>4 \wedge x\\ot=5\\D:x\in(4,5)\cup(5,\infty)\\\\(\log(x-3)\cdot \log x)/(\log(x-4))\leq0\\\\\log(x-3)\cdot \log x \cdot \log (x-4)\leq0\\\\x_0=4 \vee x_0=1 \vee x_0=5\\\\x\in(-\infty,1\rangle\cup\langle4,5\rangle\\\\\\x\in(-\infty,1\rangle\cup\langle4,5\rangle \wedge x\in(4,5)\cup(5,\infty)\\\\\boxed{\boxed{x\in(4,5)}}`

Answer 2

The given equation is

log(x-3)·log(x)

---------------------- ≤ 0

log(x-4)

As
`\log1=0`,

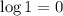So, we can write the above equation as

log(x-3)·log(x) ≤ 0 ∧ log(x-4)≥0[ if 1/a≤0, then a≥0]

Now, either log(x-3)≤ 0 ∨ log(x) ≤ 0 ∨ log(x-4)≥0

Now replacing 0 by
`\log1`.

The above equation becomes

log(x-3)≤
`\log1` ∧ log(x) ≤
`\log1` ∧ log(x-4)≥
`\log1`

Cancelling log from both sides of all the three equations

⇒ x-3≤1 ∧ x≤1 ∧ x-4≥1

⇒x≤4 ∧ x≤1 ∧ x≥5

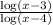`(\log(x-3))/(\log(x-4))` [ if,
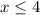`x\leq4`this expression has no meaning, so for this expression to exist,
`x\geq 5` ]

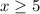Combining all the three solution , the result of the equation is

0≤ x≤1 for
`\log x \text {and } x> 4 for (\log(x-3))/(\log(x-4))`

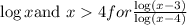
Why i have written this because the whole expression should be less than zero, so when 0≤ x≤1 ,
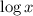`\log x` becomes negative and when x>4 the expression
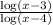`(\log(x-3))/(\log(x-4))` will be positive.