To find the coordinate of A you can first determine the coordinate of D and apply the midpoint rule.
And to find the coordinates of D you must solve equations of AC and BD simultaneously.
AC has equation
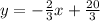
Or
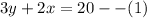
BD has equation
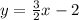
Or
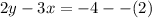
Multiply equation (1) by 2 and multiply equation (2) by 3 to obtain,
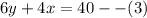
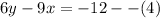
Equation (3) minus equation (4)
gives
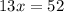
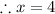
Putting the value of x=4 in equation (4) gives
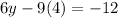
This implies that


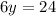
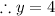
Solving the equations of AC and BD simultaneously give the coordinates of D to be;
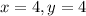
Let
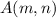
be the coordinates.
Since D is the midpoint of AC
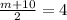
and
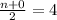
Solving for m and n, we have
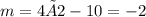
And
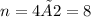
Therefore A has coordinates
[tex] (-2,8)/tex]