Let us rewrite the two lines in slope intercept form to obtain,
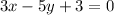
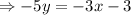
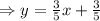
For the second equation too, we have,

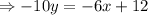
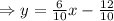

The two slopes are equal. this means the two lines are parallel. We apply the formula for finding the distance between 2 parallel lines. This formula is given by
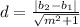
Where

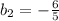
and
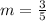
We substitute into the formula to obtain,
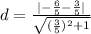
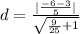
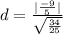
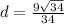
Therefore the distance between the two lines is approximately 1.5 units.