Answer:
(2,2)
Explanation:
Let's assume the four vertices of square be A(7,2), B(7,7), C(2,7) and D(x,y).
Now coordinates of vertices D needs to be found. For that use the following property of a square:
- Diagonal of square bisect each other.
Refer to figure 1 to for understanding below calculations.
Since diagonal AC and BD bisect each other at point O(p,q). Therefore O is the mid-point of both AC and BD.
Now since O is mid-point of AC. Therefore,
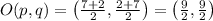
Also since O is mid-point of BD. Therefore,
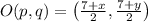
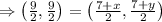
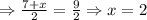
Similarly,
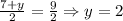
Thus coordinates of D are (2,2)