k =
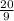 and b =
and b =

Given 2 points that lie on the graph of y = kx + b then the coordinates of these points will make the equation true. Substituting the coordinates into the equation allows us to find k and b
(2, 10) → 10 = 2k + b → (1)
( - 7, - 10) → - 10 = - 7k + b → (2)
subtracting (2) from (1) term by term gives
(10 - (- 10)) = (2k - (- 7k)) + (b - b)
20 = 9k → ( divide both sides by 9)
k =
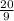
Substitute this value into ( 1) or (2) and solve for b
(1) → 10 = (2 ×
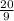 ) + b
) + b
hence b =
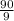 -
-
 =
=
