Question

In the isosceles △ABC m∠ACB=120° and AD is an altitude to leg BC . What is the distance from D to base AB , if CD=4cm?

Answer 1

DH = 6 cm

Explanation:

DC is 4 cm

Triangle DAC is a 30-60-90 Triangle

AC = 8

DA = 4 Root 3

DAH is a 30-60-90 Triangle

AH = 2 Root 3

DH = 2 Root 3 * Root 3 = 2*3= 6 cm

Answer 2

If ΔACB is an isosceles triangle, then ∠A ≅ ∠B and AC ≅ CB

Since ∠C = 120° and ∠A + ∠B + ∠C = 180°, then ∠A = 30° and ∠B = 30°

Next, look at ΔADB. ∠A + ∠D + ∠B = 180°, so ∠A + 90° + 30° = 180° ⇒ ∠A = 30°

Now look at ΔADC. Since ∠A = 30° in ΔACB, and ∠A = 60° in ΔADB, then ∠A = 30° in ΔADC per angle addition postulate.

Now that we have shown that ΔADB and ΔADC are 30-60-90 triangles, we can use that formula to calculate the side lengths.

CD = 4 cm (given) so AC = 2(4 cm) = 8 cm

Since AC ≅ BC, then BC = 8 cm. Therefore, BD = 4 + 8 = 12 by segment addition postulate.

Lastly, look at ΔBHD. Since ∠B = 30° and ∠H = 90°, then ∠D = 60°. So, ΔBHD is also a 30-60-90 triangle.

BD = 12 cm, so HD =
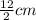`(12)/(2)cm` = 6 cm

Answer: 6 cm