Part a.
The domain is the set of x values such that
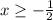 , basically x can be equal to -1/2 or it can be larger than -1/2. To get this answer, you solve
, basically x can be equal to -1/2 or it can be larger than -1/2. To get this answer, you solve
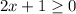 for x (subtract 1 from both sides; then divide both sides by 2). I set 2x+1 larger or equal to 0 because we want to avoid the stuff under the square root to be negative.
for x (subtract 1 from both sides; then divide both sides by 2). I set 2x+1 larger or equal to 0 because we want to avoid the stuff under the square root to be negative.
If you want the domain in interval notation, then it would be
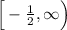 which means the interval starts at -1/2 (including -1/2) and then it stops at infinity. So technically it never stops and goes on forever to the right.
which means the interval starts at -1/2 (including -1/2) and then it stops at infinity. So technically it never stops and goes on forever to the right.
-----------------------
Part b.
I'm going to use "sqrt" as shorthand for "square root"
f(x) = sqrt(2x+1)
f(10) = sqrt(2*10+1) ... every x replaced by 10
f(10) = sqrt(20+1)
f(10) = sqrt(21)
f(10) = 4.58257569 which is approximate
-----------------------
Part c.
f(x) = sqrt(2x+1)
f(x) = sqrt(2(x)+1)
f(x+2a) = sqrt(2(x+2a)+1) ... every x replaced by (x+2a)
f(x+2a) = sqrt(2x+4a+1) .... distribute
we can't simplify any further