We know that the number of users triple each day
Let number of users on day 1 be x
⇒ Users on day 2 =
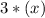 = 3x
= 3x
and Users on day 3 =
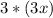 = 9x
= 9x
And so on...
% Increase in users from day 1 to day 2 =
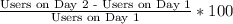
⇒ % Increase in users from day 1 to day 2 =
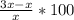
⇒ % Increase in users from day 1 to day 2 =
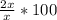
⇒ % Increase in users from day 1 to day 2 = 200%
Similarly,
% Increase in users from day 2 to day 3 =
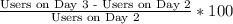
⇒ % Increase in users from day 2 to day 3 =
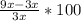
⇒ % Increase in users from day 2 to day 3 =
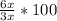
⇒ % Increase in users from day 2 to day 3 = 200%
Hence, we can see that the percentage increase each day is 200%