A car is moving at a fixed speed. The distance D that the car covers is then directly proportional to the time T it moves. If D=20 miles when T=15 minutes, write a proportion to…

Question

asked May 26, 2019 190k views

1 Answer

Vitalliuss · Answer 1 · 2019-05-30T02:38:28+0000

We were told that the distance
is directly proportional to the time
.

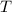We write this mathematically as,

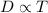
$D\propto T$

We can now introduce our constant of variation and write the equation for the direct equation as;

D=kT

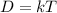
where
is the constant of variation or constant of proportionality.

We substitute
D=20 and
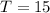T=15 , in to the equation of variation to obtain the constant of proportionality.

That is;

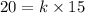
20=k*15

This implies that,

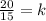
(20)/(15)=k

This simplifies to give us,

k=(4)/(3)

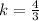
Now our equation of proportion becomes,

D=(4)/(3)

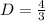
When T=20

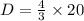
D=(4)/(3)*20

D=(80)/(3)

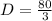
Writing this as a mixed number we obtain,

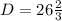
D=26(2)/(3)

This can also be rewritten as

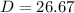D=26.67 correct to one decimal places.

Therefore the care covers
miles in
minutes.