Lets say billiard balls are arranged in rows to form an equilateral triangle, then the first row consists of 1 ball, second row consists of 2 balls, and third row consists of 3 balls, and so on. So there must be
 balls in the
balls in the
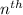 row.
row.
So, the total number of balls that forms the equilateral triangle with
 rows is:
rows is:
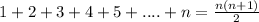
Let
 and
and
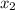 be the total number of balls in the first and second arrangements respectively.
be the total number of balls in the first and second arrangements respectively.
Then,

It has been said that there were 11 lesser balls in the second arrangement:
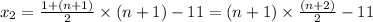
Since,
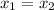
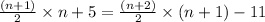
multiplying both the sides by 2
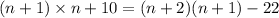
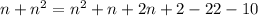

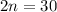

Therefore,
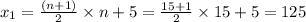
So, there were 125 balls at the set.