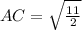Given that triangle ABC is right angle triangle. CD is altitude such that AD=BC
ABC is a right angle triangle so apply Pythogorean theorem
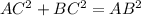
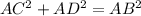 (Given that AD = BC)
(Given that AD = BC)
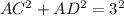 (Given that AB=3)
(Given that AB=3)
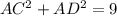 ...(i)
...(i)
ADC is a right angle triangle so apply Pythogorean theorem
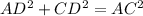
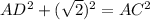
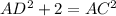
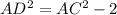 ...(ii)
...(ii)
Plug value (ii) into (i)
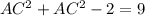
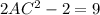
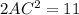
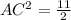
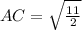
Hence final answer is