Answer:
KL =
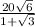 = 17.93
= 17.93
MK =
 = 25.36
= 25.36
Step-by-step explanation:
According to the Law of Sines:
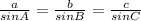
where:
A, B, and C are angles
a, b, and c are the sides opposite to the angles
First of all, let's find m∠L: the sum of the angles of a triangle is 180°, therefore
m∠K + m∠L + m∠M = 180°
m∠L = 180° - m∠K - m∠M
m∠L = 180° - 105° - 30°
m∠L = 45°
Now, we can apply the Law of Sines to our case (see picture attached):
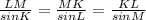
Let's solve one side at the time:
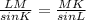
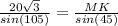
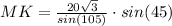
MK =
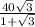 = 25.36
= 25.36
Similarily:
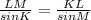
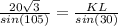
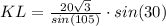
KL =
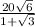 = 17.93
= 17.93