Question

Solve using the limit definition, limit as h approaches 0:

f(x)=x^3-3x+7

*I know the answer is f'(x)=3x^2-3, but I don't know how to get it using the limit definition...

Answer 1

limit formula is:
`(f(x + h) - f(x))/(h)`

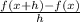
f(x + h)= (x + h)³ - 3(x + h) + 7

= x³ + 3x²h + 3xh² + h³ - 3x - 3h + 7

f(x) = x³ - 3x + 7

f(x + h) - f(x)= (a³ + 3a²h + 3ah² + h³ - 3a - 3h + 7) - (a³ - 3a + 7)

= 3x²h + 3xh² + h³ - 3h

`(f(x + h) - f(x))/(h)` =
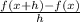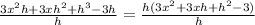`(3x^2h + 3xh^2 + h^3 - 3h)/(h) = (h(3x^2 + 3xh + h^2 - 3))/(h)` = 3x² + 3xh + h² - 3

as h approaches 0: 3x² + 3x(0) + (0)² - 3 = 3x² - 3