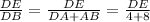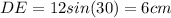Question

In the isosceles △ABC m∠ACB=120° and AD is an altitude to leg BC . What is the distance from D to base AB , if CD=4cm?

Answer 1

Correct answer is: distance from D to AB is 6cm

Solution:-

Let us assume E is the altitude drawn from D to AB.

Given that m∠ACB=120° and ABC is isosceles which means

m∠ABC=m∠BAC =
`(180-120)/(2)=30`

And AC= BC

Let AC=BC=x

Then from ΔACD , cos(∠ACD) =
`(DC)/(AC) =(4)/(x)`

Since DCB is a straight line m∠ACD+m∠ACB =180

m∠ACD = 180-m∠ACB = 60

Hence
`cos(60)=(4)/(x)`

`x=(4)/(cos60)= 8`

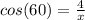
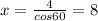
Now let us consider ΔBDE, sin(∠DBE) =
`(DE)/(DB) =(DE)/(DA+AB) = (DE)/(4+8)`

`DE = 12sin(30) = 6cm`