Answer:
Option A. The answer is incorrect; the plus sign should be a minus sign
Explanation:
we have
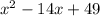
we know that
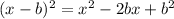
Solve for b

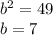
therefore
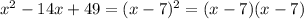
Verify each case
case A) The answer is incorrect; the plus sign should be a minus sign
The statement is true
case B) The answer is incorrect; The minus sign should be a plus sign
The statement is false
Because, the plus sign should be a minus sign
case C) The answer is incorrect; the 7's should be 14's
The statement is false
case D) The answer is correct
The statement is false