First, we are going to want to see if there are any terms we can simplify. By examining the numerators and denominators of our functions, we can see that we can remove a 3 from the denominator of the second function and the numerator of the first function. This would be represented as:
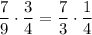
Now, we can multiply the fractions. Remember that to multiply fractions, simply multiply both the numerators over both the denominators, as shown below:
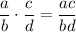
By applying this information, we can solve for the product of the fractions:
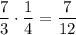
Our answer is
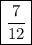 .
.